Задачу можна вирішити в O (полілог (b)).
Ми визначаємо f(d, n)як число цілих чисел до d десяткових цифр із сумою цифр менше або дорівнює n. Видно, що ця функція задана формулою

Виведемо цю функцію, починаючи з чогось більш простого.
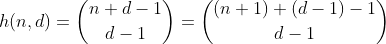
Функція h підраховує кількість способів вибору d - 1 елементів з множини, що містить n + 1 різних елементів. Це також кількість способів розділити n на d бункери, що можна легко побачити, будуючи d - 1 парканів навколо n і підсумовуючи кожен відокремлений відрізок. Приклад для n = 2, d = 3 ':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
Отже, h підраховує всі числа, що мають розрядну суму з n та d цифр. За винятком того, що він працює лише для n менше 10, оскільки цифри обмежені 0 - 9. Для того, щоб зафіксувати це для значень 10 - 19, нам потрібно відняти кількість розділів, що мають один відро з числом, більшим за 9, і я відтепер буду називати переповнені біни.
Цей термін можна обчислити шляхом повторного використання h наступним чином. Ми підраховуємо кількість способів поділу n - 10, а потім вибираємо одну з бункерів, щоб помістити 10, в результаті чого кількість розділів має один перекинутий бін. Результатом є наступна попередня функція.
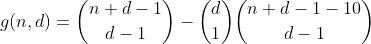
Ми продовжуємо цей шлях на n менших або рівних 29, підраховуючи всі способи розділення n - 20, потім вибираючи 2 бункери, куди ми помістимо 10-х, тим самим підраховуючи кількість розділів, що містять 2 перекинуті бункери.
Але в цей момент ми повинні бути обережними, тому що ми вже порахували розділи, що мали 2 перекинуті бункери в попередньому терміні. Мало того, але насправді ми їх перераховували двічі. Давайте скористаємося прикладом та подивимось на розділ (10,0,11) із сумою 21. У попередньому терміні ми віднімали 10, обчислювали всі розділи з решти 11 і ставили 10 в один із 3 бін. Але цього конкретного розділу можна досягти двома способами:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Оскільки ми також підраховували ці розділи один раз у першому терміні, загальна кількість перегородок з 2 перекритими бункерами становить 1 - 2 = -1, тому нам потрібно порахувати їх ще раз, додавши наступний термін.
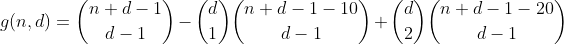
Розмірковуючи про це трохи більше, ми незабаром виявляємо, що кількість розбитків розділу з певною кількістю перекритих бункерів підраховується в конкретному терміні, можна виразити наступною таблицею (стовпець i являє собою термін i, розділи j, розділ j з j перевитратою бункери).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Так, це трикутник Паскаля. Єдиний підрахунок, який нас цікавить, - це перший рядок / стовпець, тобто кількість розділів з нульовим перекриттям. А оскільки чергування суми кожного ряду, але першого дорівнює 0 (наприклад, 1 - 4 + 6 - 4 + 1 = 0), то ми їх позбавляємося і доходимо до передостанньої формули.
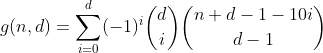
Ця функція підраховує всі числа з d цифр, що мають цифру суми n.
А тепер, що з числами з цифрою-сумою менше n? Ми можемо використовувати стандартний рецидив для біноміалів плюс індуктивний аргумент, щоб показати це
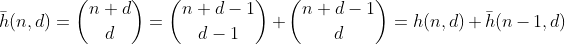
підраховує кількість розділів із знаковою сумою не більше n. І з цього f можна отримати, використовуючи ті ж аргументи, що і для g.
Використовуючи цю формулу, ми можемо, наприклад, знайти кількість важких чисел в інтервалі від 8000 до 8999 як 1000 - f(3, 20) , оскільки в цьому інтервалі є тисячі чисел, і ми повинні відняти кількість чисел із цифрою, меншою або дорівнює 28 при цьому беручи до уваги, що перша цифра вже вносить 8 до цифрної суми.
Як більш складний приклад розглянемо кількість важких чисел в інтервалі 1234..5678. Спочатку ми можемо перейти від 1234 до 1240 з кроком 1. Потім переходимо від 1240 до 1300 з кроком 10. Вищенаведена формула дає нам кількість важких чисел у кожному такому інтервалі:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Тепер ми переходимо від 1300 до 2000 з кроком 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
Від 2000 до 5000 з кроком 1000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Тепер нам доведеться знову зменшити розмір кроків, переходячи від 5000 до 5600 з кроком 100, з 5600 до 5670 в кроках 10 і, нарешті, з 5670 до 5678 в кроках 1.
Приклад реалізації Python (який тим часом отримав невеликі оптимізації та тестування):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Редагування : Замінено код оптимізованою версією (яка виглядає ще більш потворною, ніж оригінальний код). Також виправили кілька кутових справ, поки я був на ньому. heavy(1234, 100000000)займає близько моєї мілісекунди на моїй машині.
