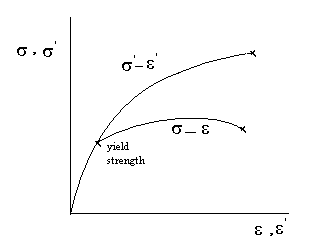Чому ми навіть використовуємо інженерний стрес?

Дивно, але цього раніше не просили, тому я, мабуть, пропускаю щось просте.

У цьому еквіваленті ми використовуємо інженерний стрес та інженерну напругу Стрес = (модуль Юнга) × (напруга). Цей екв. застосовується при аналізі згинальних балок, скручування валів і при спрацюванні. Отже, підсумкове рівняння згинання і кручення($(\frac{M}{I} = \frac{\sigma}{y})$дасть нам значення інженерного напруження, але не значення напруження.$(\frac{T}{I} = \frac{\tau}{r})$

Чому ми розглядаємо інженерний стрес замість справжнього напруження, тоді як знаємо, що він не дасть правильного значення напруги?

Я читаю кілька речей:

1. Важко виміряти.
2. Не велика різниця, і ми можемо просто застосувати Фактор безпеки.
3. "Ми не вважаємо, що матеріали змінюють площу поперечного перерізу після завантаження, оскільки ми проектуємо, щоб не було пластичної деформації, найбільш важливою є пружна область, тому те, що відбувається після пропорційної межі, не важливо"

По-перше, 1 і 2 не є для мене справжніми причинами. Число 3 здається правдоподібним, оскільки ми завжди проектуємо в еластичній області, але чи це це? Чи інженерний штам навіть надає дійсну інформацію після пропорційного обмеження?

Ми використовуємо інженерний деформацію, навіть якщо це не "правильне" значення, оскільки в більшості випадків, особливо в пружному режимі, інженерний штам відрізняється від істинного деформації.

Що стосується лінійних еластичних матеріалів Хукея, то, як правило, деформація на межі пружності дуже мала. Навіть найміцніші сталі, наприклад, мають верхню межу при роботі холоду приблизно . Модуль сталі приблизно E = 200 × 10 9 Па . Таким чином ε el = 0,005 = 0,5 % для найміцніших сталей. Тож при настанні пластичної деформації інженерна деформація становить 0,5 % . Багато корисних еластичних матеріалів мають значно менші інженерні деформації у своїх пружних межах.$\sigma_{\textrm{el}}=1\times 10^{9}\ \textrm{Pa}$$E=200\times 10^{9}\ \textrm{Pa}$$\varepsilon_{\textrm{el}}=0.005=0.5\%$$0.5\%$

Для ізотропного, гукового еластичного твердого тіла справедливо наступне

$$\varepsilon_{x_{1}} = \frac{1}{E}\left[\sigma_{x_{1}}-\nu\left(\sigma_{x_{2}}+\sigma_{x_{3}}\right)\right]$$

$x_{i}$$\sigma_{x_{2}}=\sigma_{x_{3}}=0$$\varepsilon_{x_{2}}=\varepsilon_{x_{3}}=-\frac{\sigma_{\textrm{el}}\nu}{E}=-\nu\varepsilon_{\textrm{el}}$$\nu$$0.0015$$(1-0.0015)^{2}A_{0}$$0.997$

$\frac{1}{0.997}$$1.003$$0.3\%$

Хоча вищезазначений аналіз є досить корисним для лінійно еластичних твердих тіл Гукея, він не дуже добре підходить для полімерів та біологічних матеріалів. Такі матеріали, як правило, в'язкопружні (або інший клас матеріалу цілком), і тому підкоряються різним правилам у своїй поведінці. Справжній штам також досить дивовижно відрізняється від інженерної деформації в пластичному режимі, про що свідчить наступний сюжет (знайдений тут )

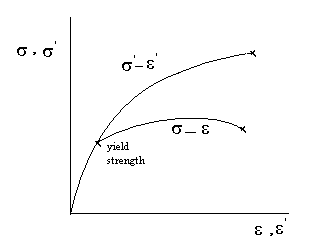
Щодо ваших балів:

1. Вимірювання змін до площі поперечного перерізу в процесі деформації є важким. Він вимагає ретельного розміщення відкаліброваних приладів на точно оброблених випробувальних зразках. Можна було використовувати тензодатчики, розміщені з боків натяжної штанги для вимірювання бічного напруження в одноосному натягу та стискуванні в апараті для випробування на розтяг . Отримання статистично значущих результатів вимагає багатьох зразків, а також значних витрат часу, зусиль та витрат.

2. $0.3\%$

3. Ідея, що ми можемо ігнорувати що-небудь поза кінцем еластичного режиму, або що ми завжди розробляємо для еластичного режиму, не відповідає дійсності. Пластичну деформацію часто варто вивчити. Моделювання безперервних процесів формування форми, таких як прокат, малювання, екструдування тощо, вимагає глибокого розуміння механіки пластичної деформації для успішного виконання, і для цього справжнє напруження та справжнє напруження є неоціненними. Спеціально для малювання дроту див. (Цей pdf ) та знайдіть рівняння 7. Пластична деформація також корисна для моделювання матеріалів, які повинні постійно деформуватися у деяких випадках, що очікуються, наприклад, на панелі кузова автомобіля та компоненти рами під час зіткнення. Пластична деформація корисна тим, що вона поглинає кінетичну енергію.

Редагувати: Вибачте, я фактично не відповів на питання, що було стрес. Однак має бути досить зрозуміло, що ті ж самі точки стосуються напруги, що і для деформації, враховуючи їх лінійну залежність в пружному режимі. Знову ж таки, в пластичному режимі можуть бути великі варіації.

Додавання до відповіді @ starrise:

Що стосується вашого звільнення з причин 1 і 2, ви забуваєте розглянути аналіз витрат і вигод щодо них. Як показав @starrise у своїй відповіді, різниця зазвичай не суттєва (хоча інші матеріали, як правило, мають більші відмінності).

$\pm6\%$ $\pm15\%$

Отже, який сенс розглядати справжнє напруження в повсякденній інженерній практиці, якщо всі інші властивості (включаючи міцність пружності та розміри поперечного перерізу) матимуть випадкові коливання, які, окрім певних, не зможуть усунути "помилку" через використання інженерний штам замість справжнього штаму?