Як думати про ворота Z у сфері Bloch?

11

Я розгублений, як зрозуміти $Z$ ворота в сфері Блоха.

Розглядаючи матрицю $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ зрозуміло, що $Z|0\rangle = |0\rangle$ і $Z|1\rangle = -|1\rangle$ .

Це пояснюється тут , що $Z$ ворота є $\pi$ обертання навколо $Z$ вісь. Потім, як я маю зрозуміти $Z|1\rangle = -|1\rangle$ ? З тих пір $|1\rangle$ це південний полюс, я вважаю, що це природно думати $\pi$ обертання навколо $Z$ вісь нічого не робить.

quantum-gate bloch-sphere

— Бік
джерело

7

Спосіб думати про сферу Блоха полягає в матриці щільності для держави. $Z$ що діє на будь-який $|0\rangle\langle 0|$ або $|1\rangle\langle 1|$ нічого не робить, як це стосується будь-якої матриці діагональної щільності. Щоб побачити ефект обертання, потрібно подивитися, як змінюється будь-яка матриця недіагональної щільності $Z$ , як от $|+\rangle\langle +|$ .

— DaftWullie
джерело

8

$|1\rangle$ і $-|1\rangle$ присвоюються одній і тій же точці в сфері Блоха, оскільки вони рівні до глобальної фази . Алгебраїчно: $|1\rangle \equiv -|1\rangle$ де $\equiv$ означає "рівний до глобальної фази". Значення є якесь $\theta$ такий як $-|1\rangle = e^{i \theta} |1\rangle$ .

Те, що вас бентежить, це те, що, незважаючи на те, що $|0\rangle \equiv Z |0\rangle$ і $|1\rangle \equiv Z |1\rangle$ , це не вірно для лінійних комбінацій двох. Наприклад, $Z |+\rangle \not\equiv Z |+\rangle$ незважаючи на $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$ .

— Крейг Гідні
джерело

2

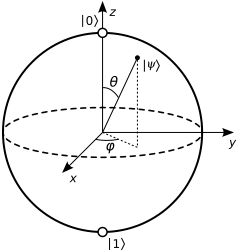
Відповідно до Вікіпедії , ми можемо записати будь-який чистий стан як

| ψ ⟩ = \cos (\frac{θ}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{θ}{2}) | 1 ⟩

$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$

Де $\theta$ і $\phi$ - кути на сферу Блоха:

Практично будь-яка точка на поверхні (тобто чистий стан) має унікальне уявлення щодо кутів, за винятком полюсів. Як і на Землі, Південний полюс не має чітко визначеної довготи (будь-яка довгота працює однаково) для $|1 \rangle$ констатувати будь-яку фазу $\phi$ означає те саме. "Широта" $\theta$ тут $\pi$ , підключимо це до рівняння:

| 1 ⟩ = \cos (\frac{π}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{π}{2}) | 1 ⟩ =

$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$

= 0 + e^{i ϕ} | 1 ⟩

$= 0 + e^{i \phi} |1 \rangle$

Якщо ви знайомі з особою Ейлера, ви, ймовірно, впізнаєте $e^{i \phi}$ як обертання в складній площині. Зокрема, оскільки $Z$ є обертанням для $\phi = \pi$ , ми отримуємо знаменитий $e^{i \pi} = -1$ , нарешті, прибуваючи $|1 \rangle = - |1 \rangle$ .

— Норріус
джерело

1

Це неправильно. Написання

| 1 ⟩ = - | 1 ⟩

$|1\rangle=-|1\rangle$ вводить в оману: це рівнозначні стани тим, що вони відрізняються лише глобальною фазою, але це не означає, що державні вектори однакові. Цей результат ви отримуєте, тому що ви припускаєте, що між векторами стану та точками на сфері Блоха існує біекція, що не так. Бієкція стоїть між точками на сфері Блоха і станами, описаними як матриці щільності

— glS

@glS Дякую,

1 = - 1

$1=-1$ що випливає з цього, здавалося, рибним. Чи є сенс вдосконалювати цю відповідь з вашої точки зору, чи це безнадійно неправильно?

— Норріус

це ваш дзвінок =). Я вважаю, що правильна відповідь - це відповідь, яку дав Дафтваллі (я вважаю, що у особи, що ставить запитання, було подібне неправильне уявлення, як у вашій відповіді). Я не бачу нічого сказати з цього питання

— glS