Що означає клиноподібна форма сюжету PCA?

У своїй роботі по автоассоціатор для тексту класифікації Хінтон і Салахутдинов показав сюжет , отриманий на 2-мірної LSA (який тісно пов'язаний з PCA) .

Застосовуючи PCA до абсолютно різних злегка високих розмірних даних, я отримав подібний зовнішній вигляд: (за винятком цього випадку я дуже хотів знати, чи є якась внутрішня структура).

Якщо ми подаємо випадкові дані в PCA, ми отримаємо диск у формі диска, тому ця форма клиноподібної форми не є випадковою. Чи означає це щось саме по собі?

Якщо припустимо, що змінні є позитивними чи негативними, то краї краю - це лише точки, за якими дані ставали б 0 або негативними відповідно. Оскільки такі дані реального життя, як правило, перекошені правильно, ми бачимо більшу щільність точок на нижньому кінці їх розподілу і, отже, більшу щільність у "точці" клина.

Більш загально, PCA - це просто обертання даних, а обмеження щодо цих даних, як правило, будуть видні в основних компонентах таким же чином, як показано в питанні.

Ось приклад з використанням декількох змінних, що нормалізуються журналом:

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

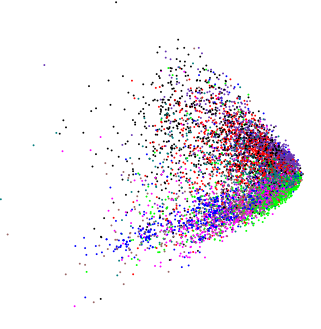
Залежно від обертання, що має на увазі перші два комп'ютери, ви можете побачити клин або ви можете дещо іншу версію, показати тут у 3d, використовуючи ( ordirgl()замість plot())

Тут у 3d ми бачимо безліч шипів, що виступають з центральної маси.

Для випадкових змінних Гаусса ($X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$) де кожен має однакове середнє значення та дисперсію, ми бачимо сферу точок

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

А для рівномірних позитивних випадкових величин ми бачимо куб

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

Зауважте, що тут для ілюстрації я показую уніформу за допомогою лише 3 випадкових змінних, отже точки описують куб у 3d. З більшими розмірами / більшою кількістю змінних ми не можемо представити 5d гіперкуб в ідеалі в 3d, і, отже, чітка форма "куба" дещо спотворюється. Подібні проблеми впливають на інші наведені приклади, але все ще легко побачити обмеження в цих прикладах.

Для ваших даних перетворення змінних журналів до PCA потягнуло б хвости та розтягнуло зведені дані так само, як ви могли б використовувати таке перетворення в лінійній регресії.

Інші форми можуть з'являтися на ділянках PCA; одна така форма являє собою артефакт метричного зображення, що зберігається в PCA і відомий як підкова . Для даних з довгим або домінуючим градієнтом (зразки, розташовані вздовж одного виміру зі змінними, що збільшуються від 0 до максимуму, а потім знову зменшуються до 0 вздовж частин даних, добре відомі для створення таких артефактів. Поміркуйте.

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

яка дає крайню підкову, де точки на кінцях осей відгинаються назад в середину.