У чому полягає теорема Байєса?

Які основні ідеї, тобто поняття, пов'язані з теоремою Байєса ? Я не прошу жодних похідних складних математичних позначень.

Теорема Байєса - відносно простий, але фундаментальний результат теорії ймовірностей, який дозволяє обчислити певні умовні ймовірності. Умовні ймовірності - це лише ті ймовірності, які відображають вплив однієї події на ймовірність іншої.

Простіше кажучи, у своїй найвідомішій формі він стверджує, що ймовірність гіпотези з новими даними ( P (H | D) ; називається задньою ймовірністю) дорівнює такому рівнянню: ймовірності спостережуваних даних, що даються гіпотезою ( P (D | H) ; називається умовною ймовірністю), що розраховує імовірність істинності теорії до появи нових доказів ( P (H) ; називається попередньою ймовірністю H), поділену на ймовірність бачити ці дані, період ( P (D ); називається граничною ймовірністю D).

Формально рівняння виглядає так:

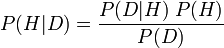
Значення теореми Байєса багато в чому пов'язане з її правильним використанням як точки суперечки між школами думки щодо вірогідності. Для суб'єктивного байєсівця (який трактує ймовірність як суб'єктивну ступінь віри) теорема Байєса є основою для теоретичного тестування, вибору теорії та інших практик, шляхом включення їх суб'єктивних суджень про ймовірність у рівняння та запуску з ним. Для частофілістів (що трактує ймовірність як обмеження відносних частот ), використання теореми Байєса є зловживанням, і вони прагнуть замість цього використовувати значущі (не суб'єктивні) пріори (як це роблять об'єктивні байєси під іншим тлумаченням ймовірності).

Вибачте, але, мабуть, тут є деяка плутанина: теорема Байєса не підходить для обговорення постійної дискусії про байєсівсько- частотологів . Це теорема, яка узгоджується з обома школами думки (враховуючи, що вона відповідає аксіомам ймовірності Колмогорова).

Звичайно, теорема Байєса є ядром байєсівської статистики, але сама теорема є універсальною. Сутичка між часто відвідувачами та байєсами стосується того, як можна визначити попередні розподіли чи ні.

Отже, якщо мова йде про теорему Байєса (а не про баєсівську статистику):

Теорема Байєса визначає, як можна обчислити конкретні умовні ймовірності. Уявімо, наприклад, що ви знаєте: ймовірність виникнення у кого-небудь симптому А, враховуючи, що у них захворювання X p (A | X); ймовірність того, що хтось взагалі має хворобу X p (X); ймовірність того, що хтось взагалі має симптом A p (A). за допомогою цих 3 даних можна обчислити ймовірність того, що хтось захворіє на хворобу Х, враховуючи, що у них є симпотома A p (X | A).

Теорема Байєса - це спосіб повернути умовну ймовірність на іншу умовну ймовірність P ( B | A ) .$P(A|B)$$P(B|A)$

Каменем спотикання для деяких є значення . Це спосіб зменшити простір можливих подій, розглядаючи лише ті події, де A безумовно відбувається (або це правда). Так, наприклад, ймовірність того, що кинуті, справедливі землі з кістки, що показують шість, P ( кубики мають шість ) , дорівнює 1/6, однак ймовірність того, що кістки висаджують шість, враховуючи, що вона висадила парне число, P ( кістки землі шість | кубики землі навіть ) , становить 1/3.$P(B|A)$$A$$P(\mbox{dice lands six})$$P(\mbox{dice lands six}|\mbox{dice lands even})$

Ви можете самостійно отримати теорему Байєса. Почніть з визначення співвідношення умовної ймовірності:

$P(B|A) = \frac{P(AB)}{P(A)}$

де є спільною ймовірністю A і B і P ( A ) є граничною ймовірністю A .$P(AB)$$A$$B$$P(A)$$A$

Наразі формула не посилається на , тому запишемо також визначення цього:$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

$P(AB) = P(BA)$$AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

$P(B|A)$$P(AB)$

$P(AB) = P(A|B)P(B)$

і ей престо:

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

Щодо сенсу в тому, щоб обертати умовну ймовірність таким чином, розглянемо загальний приклад спроби встановити ймовірність того, що хтось має захворювання, враховуючи, що у них є симптом, тобто ми знаємо, що у них є симптом - ми можемо просто бачити це - але ми не можемо бути впевнені, чи є у них хвороба, і чи потрібно це робити. Почну з формули і повернусь назад.

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

Отже, щоб розібратися, потрібно знати попередню ймовірність симптому, попередню ймовірність захворювання (тобто, наскільки поширеними чи рідкісними є симптом та захворювання), а також ймовірність того, що у когось є симптом, якщо ми знаємо, що хтось має захворювання (наприклад, за допомогою дорогих трудомістких лабораторних тестів).

Це може бути набагато складніше, ніж це, наприклад, якщо у вас є численні захворювання та симптоми, але ідея та ж. Навіть більш загально, теорема Байєса часто виникає, якщо у вас є теорія ймовірності взаємозв'язків між причинами (наприклад, хворобами) та наслідками (наприклад, симптомами) і вам потрібно міркувати назад (наприклад, ви бачите деякі симптоми, від яких ви хочете зробити висновок про основне захворювання).

Існує дві основні школи думки статистики: частістська та байєсівська .

Теорема Байєса пов'язана з останньою, і її можна розглядати як спосіб розуміння того, як на ймовірність того, що теорія є істинною, впливає новий доказ. Це відомо як умовна ймовірність. Ви можете поглянути на це, щоб отримати ручку з математики.

Дозвольте дати вам дуже інтуїтивне розуміння. Припустимо, що ти кидаєш монету в 10 разів і отримуєш 8 голів та 2 хвости. Питання, яке б вам спало на думку, полягає в тому, чи є ця монета упереджена до голови чи ні.

Тепер, якщо ви йдете за загальноприйнятими означеннями або частолістським підходом ймовірності, ви можете сказати, що монета є неупередженою, і це надзвичайне явище. Звідси ви зробите висновок, що можливість отримати голову поруч з кидком також становить 50%.

Але припустимо, що ви баєц. Ви насправді подумаєте, що оскільки у вас є надзвичайно велика кількість голів, монета має ухил у бік голови. Існують методи обчислення цього можливого зміщення. Ви б їх обчислили, і тоді, коли ви кинете монету наступного разу, ви неодмінно подзвоните в голову.

Отже, байєсівська ймовірність - це віра, яку ви розвиваєте на основі даних, які ви спостерігаєте. Я сподіваюся, що це було досить просто.

Теорема Байєса пов'язує дві ідеї: ймовірність та ймовірність. Ймовірність говорить: з огляду на цю модель, це результати. Отже: якщо ви отримаєте справедливу монету, я отримаю голови 50% часу. Ймовірність говорить: з огляду на ці результати, це те, що ми можемо сказати про модель. Отже: якщо ви кинете монету в 100 разів і отримаєте 88 голів (взяти на попередній приклад і зробити її більш крайньою), то ймовірність правильної моделі монети не така вже й велика.

Одним із стандартних прикладів, який використовується для ілюстрації теореми Байєса, є ідея тестування на хворобу: якщо ви складете тест, що на 95% точний на захворювання, яке має 1 10000 населення, і ви тестуєте позитивний, які шанси що у вас захворювання?

Наївна відповідь - 95%, але це ігнорує питання про те, що 5% тестів на 9999 з 10000 людей дадуть хибний позитив. Тож ваші шанси виникнення захворювання набагато нижчі, ніж 95%.

Моє використання невиразної фрази "які шанси" є навмисною. Використовувати мову ймовірності / ймовірності: ймовірність того, що тест є точним, становить 95%, але те, що ви хочете знати, - це ймовірність наявності у вас захворювання.

Трохи поза темою: Іншим класичним прикладом, який теорема Байєса використовується для вирішення у всіх підручниках, є проблема Монті Холла: Ви на вікторині. За однією з трьох дверей є приз. Ви обираєте двері. Ведучий відкриває три двері, щоб не виявити жодного призу. Ви повинні перейти на двері, надавши шанс?

Мені подобається переформулювання питання (люб’язно надано посилання нижче): ви на вікторині. За однією з мільйонів дверей є приз. Ви обираєте двері. Ведучий відкриває всі інші двері, крім дверей 104632, щоб не виявити жодного призу. Ви повинні перейти на двері 104632?

Моя улюблена книга, в якій дуже багато обговорюється теорема Байєса, з точки зору Байєса, - це "Інформаційна теорія, алгоритми виведення та навчання" Девіда Дж. Маккея. Це книга Кембриджського університету у пресі, ISBN-13: 9780521642989. Моя відповідь - це (я сподіваюсь) дистиляція виду дискусій, про які йдеться в книзі. (Звичайні правила діють: я не маю прихильності до автора, мені просто подобається книга).

Теорема Байєса у своїй найбільш очевидній формі - це просто повторне твердження двох речей:

1. $P(HD|I)=P(DH|I)$
2. $P(HD|I)=P(H|I)P(D|HI)$

Отже, використовуючи симетрію:

$P(D|I) \neq 0$$P(D|I)$

Так це все? Як щось таке просте може бути таким приголомшливим? Як і в більшості речей, "її подорож важливіша за призначенням". Теорема Байєса породжується через аргументи, які ведуть до цього.

$P(H|I)=1-P(\overline{H}|I)$

Тепер "правилом" дедуктивної логіки є те, що якщо у вас є стосунки "A означає B", то ви також маєте "Not B означає не A". Отже, у нас "послідовне міркування передбачає теорему Байєса". Це означає, що "теорема Не Байєса не передбачає не послідовних міркувань". тобто якщо ваш результат не є рівнозначним байєсівському результату за деякими попередніми та ймовірними, тоді ви міркуєте непослідовно.

Цей результат отримав назву теореми Кокса і був доведений в "Алгебрі ймовірного висновку" в 40-х роках. Більш недавнє виведення дано в теорії Proability: Логіка науки.

Мені дуже подобається вступ Кевіна Мерфі до теорії Байєса http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html

Цитата тут із статті економіста:

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

Суть байєсівського підходу полягає у наданні математичного правила, що пояснює, як слід змінити існуючі переконання з огляду на нові докази. Іншими словами, це дозволяє вченим поєднувати нові дані з наявними знаннями чи знаннями. Канонічним прикладом є уявити, що передчасне новонароджене спостерігає за своїм першим заходом сонця і замислюється про те, чи встане сонце знову чи ні. Він призначає однакові попередні ймовірності обом можливим результатам, і представляє це, поміщаючи в мішок один білий і один чорний мармур. Наступного дня, коли сходить сонце, дитина кладе в сумку ще один білий мармур. Ймовірність того, що мармур, який випадковим чином вирвався з сумки, стане білим (тобто ступінь віри дитини у майбутні схід сонця), таким чином, перейшов від пів до двох третин. Після сходу сонця наступного дня, дитина додає ще один білий мармур, і ймовірність (і, таким чином, ступінь віри) переходить від двох третин до трьох чвертів. І так далі. Поступово початкова віра в те, що сонце так само ймовірно, що не встає щоранку, змінюється, щоб стати майже впевненістю, що сонце завжди вставатиме.