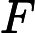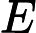Наскільки складно використовувати підхід Мулмулі-Сохоні GCT, щоб показати відомі * розділення складності?

У цьому доступі Джоша Грохова на веб- журналі про складності він повідомляє про нещодавній семінар, присвячений GCT, який відбувся в Принстоні в липні. Декілька присутніх стверджували, що ми повинні використовувати GCT для атаки легших проблем, ніж vs. N P , щоб створити інтуїцію та побачити, чи має метод потенціал.$\mathsf{P}$$\mathsf{NP}$

Питання, яке мене клопоче:

Чи можна використовувати GCT для показу відомих розділень, таких як або L ≠ P S P A C E ?$\mathsf{P} \neq \mathsf{EXP}$$\mathsf{L} \neq \mathsf{PSPACE}$

Чи щось на зразок $\mathsf{L} \neq \mathsf{PSPACE}$

1. Навіть не має сенсу в контексті ДКТ, або
2. Цілком тривіально і нецікаво в рамках ДКТ, або
3. Привести до гіпотез так само важко, як проти N P ?$\mathsf{P}$$\mathsf{NP}$

Коротка відповідь: напевно, немає (1), точно не (2), а можливо (3).

Це те, про що я думав уже поза деяким часом. По-перше, у певному сенсі GCT насправді спрямований на надання нижчих меж обчислювальних функцій, а не на проблеми з рішенням. Але ваше запитання має сенс для функції класу версій , P , P S P A C E і E X P .$L$$P$$PSPACE$$EXP$

По-друге, фактично довести булеві версії - ті, яких ми знаємо і любимо, як - напевно, неймовірно складно в GCT-підході, оскільки це вимагало б використання модульної теорії представлення (теорія представлення над скінченним поля), що недостатньо добре зрозуміло в будь-якому контексті. $FP \neq FEXP$

Але розумна мета може полягати у використанні GCT , щоб довести алгебраїчний аналог .$FP \neq FEXP$

Щоб перейти до вашого питання: Я вважаю, що ці питання можна сформулювати в контексті ДКТ, хоча не відразу зрозуміло, як. Більш-менш потрібна функція, яка є повною для класу і характеризується її симетрією; додатковий бонус, якщо теорію представлення, пов'язану з функцією, легко зрозуміти, але це останнє зазвичай досить складно.

Навіть після того, як питання сформульовані в контексті ДКТ, я не маю уявлення, наскільки складно буде використовувати ГКТ для доказування (алгебраїчних аналогів) і т. Д. Репрезентативно-теоретичні гіпотези, які виникнуть у цих контекстах ймовірно, матиме дуже схожий аромат на ті, що виникають у P vs N $FP \neq FEXP$$P$$NP$або постійний проти детермінантний. Можна сподіватися, що класичні докази цих результатів поділу можуть дати деяке уявлення про те, як знайти теоретично-представницькі "перешкоди", необхідні для доказу ГКТ. Однак докази тверджень, які ви згадуєте, - це всі теореми ієрархії, засновані на діагоналізації, і я не бачу, як діагоналізація справді дасть вам багато розуміння теорії представлення, пов'язаної з функцією, повною для (алгебраїчного аналога) , скажімо. З іншого боку, я ще не бачив, як сформулювати F E X P у контексті ДКТ, тому сказати трохи рано.$FEXP$$FEXP$

Нарешті, як я вже згадував у цій публікації в блозі, Пітер Бургіссер та Крістіан Ікенмайєр намагалися знову довести нижню межу множення матричного множення (що було доведено 7 у 2006 р. Джозефом Ландсбергом). Вони змогли показати прикордонний принаймні 6 за допомогою комп'ютерного пошуку перешкод GCT. Оновлення квітня 2013 року : з тих пір їм вдалося відновити результат Ландсберга за допомогою перешкод GCT та показати асимптотику 3$2 \times 2$нижня межа матричного множення$\frac{3}{2}n^2 - 2$за допомогою таких перешкод. Незважаючи на те, що GCT поки не відтворював відому нижню межу множення матриць, це дає можливість пошуку за комп'ютером більш ефективним, ніж альтернативний (який би залучав бази Grobner, які в гіршому випадку мають подвійний показник часу). У своїх бесідах на семінарі і Петро, ​​і Крістіан зазначали (правильно, я б сказав), що те, що ми справді сподіваємося отримати обчислення невеликих прикладів, - це не відновлення відомих нижніх меж, а деякерозуміння,яке дозволить нам використовувати їх методи доведенняновихнижчих меж.

Приємне про GCT в контексті множення матриць полягає в тому, що методика легко узагальнює від до 3 × 3 матричне множення (хоча обчислення перешкод діючими методами очевидно стає дорожчим), тоді як підхід Ландсберга здається дуже важким для реалізації навіть для випадку 3 × 3 . Аналогічну річ можна сказати і про розділення класів складності, які ви згадуєте: GCT є загальним, що може застосовуватися не лише до відомих результатів, таких як F P ≠ F E X P , але і до невідомих, таких як P $2 \times 2$$3 \times 3$$3 \times 3$$FP \neq FEXP$ , тоді як ми знаємо, що діагоналізація не робить.$P \neq NP$

На arXiv Joshua Grochow з'явився новий документ , який показує, як вкласти кілька відомих методів нижньої межі в рамки GCT і, здається, він дещо відповідає на ваше запитання.

(Це здебільшого просто коментар, але ніхто не помітить коментар, тому я публікую його як відповідь.)

Уніфікація та узагальнення відомих нижніх меж за допомогою теорії геометричної складності

Джошуа А. Грохов

$AC^0[p]$внаслідок чого це природне об'єднання та широке узагальнення відомих результатів. Це також показує, що основи ДКТ є принаймні настільки потужними, як відомі методи, і дає багато нових доказів концепції того, що ГКТ дійсно може забезпечити значні асимптотичні нижні межі. Ця нова точка зору також відкриває можливість плідної двосторонньої взаємодії між попередніми результатами та новими методами ГКТ; ми надаємо кілька конкретних пропозицій таких взаємодій. Наприклад, теоретично-представницька точка зору GCT, природно, забезпечує нові властивості, які слід враховувати при пошуку нових нижчих меж. Ця нова точка зору також відкриває можливість плідної двосторонньої взаємодії між попередніми результатами та новими методами ГКТ; ми надаємо кілька конкретних пропозицій таких взаємодій. Наприклад, теоретично-представницька точка зору GCT, природно, забезпечує нові властивості, які слід враховувати при пошуку нових нижчих меж. Ця нова точка зору також відкриває можливість плідної двосторонньої взаємодії між попередніми результатами та новими методами ГКТ; ми надаємо кілька конкретних пропозицій таких взаємодій. Наприклад, теоретично-представницька точка зору GCT, природно, забезпечує нові властивості, які слід враховувати при пошуку нових нижчих меж.