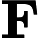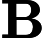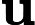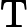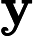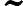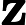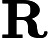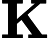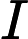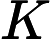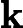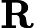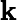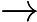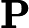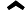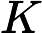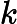Як зрозуміти, що Кальман отримує інтуїтивно?

30

Алгоритм фільтра Калмана працює наступним чином

Ініціалізуйте та . $\hat{\textbf{x}}_{0|0}$ $\textbf{P}_{0|0}$

При кожній ітерації $k=1,\dots,n$

Прогнозуйте

Прогнозована (апріорі) оцінка стану Прогнозована (апріорі) оцінка коваріації Оновити
${\hat{x}}_{k | k - 1} = F_{k} {\hat{x}}_{k - 1 | k - 1} + B_{k} u_{k}$ $\hat{\textbf{x}}_{k|k-1} = \textbf{F}_{k}\hat{\textbf{x}}_{k-1|k-1} + \textbf{B}_{k} \textbf{u}_{k}$ $P_{k | k - 1} = F_{k} P_{k - 1 | k - 1} F_{k}^{T} + Q_{k}$ $\textbf{P}_{k|k-1} = \textbf{F}_{k} \textbf{P}_{k-1|k-1} \textbf{F}_{k}^{\text{T}} + \textbf{Q}_{k}$
Інновація або вимірювання залишкова Інновація (або залишкова) коваріація Оптимальний посилення Кальмана Оновлена (a posteriori) оцінка стану Оновлено (a posteriori) оцінка коваріації
${\tilde{y}}_{k} = z_{k} - H_{k} {\hat{x}}_{k | k - 1}$ $\tilde{\textbf{y}}_k = \textbf{z}_k - \textbf{H}_k\hat{\textbf{x}}_{k|k-1}$ $S_{k} = H_{k} P_{k | k - 1} H_{k}^{T} + R_{k}$ $\textbf{S}_k = \textbf{H}_k \textbf{P}_{k|k-1} \textbf{H}_k^\text{T} + \textbf{R}_k$ $K_{k} = P_{k | k - 1} H_{k}^{T} S_{k}^{- 1}$ $\textbf{K}_k = \textbf{P}_{k|k-1}\textbf{H}_k^\text{T}\textbf{S}_k^{-1}$ ${\hat{x}}_{k | k} = {\hat{x}}_{k | k - 1} + K_{k} {\tilde{y}}_{k}$ $\hat{\textbf{x}}_{k|k} = \hat{\textbf{x}}_{k|k-1} + \textbf{K}_k\tilde{\textbf{y}}_k$ $P_{k | k} = (I - K_{k} H_{k}) P_{k | k - 1}$ $\textbf{P}_{k|k} = (I - \textbf{K}_k \textbf{H}_k) \textbf{P}_{k|k-1}$

Кальмана представляє відносну важливість помилки щодо попередньої оцінки . $K_k$ $\tilde{\textbf{y}}_k$ $\hat{\textbf{x}}_{k|k-1}$

Цікаво, як зрозуміти інтуїтивно зрозумілу формулу для отримання ? Розглянемо випадок, коли стани і виходи є скалярними, чому виграш більший, коли $K_k$

$\textbf{P}_{k|k-1}$ більший
$\textbf{H}_k$ більший
$\textbf{S}_k$ менший?

Дякую та з повагою!

kalman-filters

— Тім
джерело

На це складне питання правильно відповісти. Я спробував, але не переконаний власною відповіддю. По суті, коефіцієнт посилення контролює те, наскільки ви довіряєте вимірюванням над оцінкою, але я не можу пояснити, як цей коефіцієнт відповідає.

— Jav_Rock

18

Я знайшов хороший спосіб мислення інтуїтивно Калмана посилення . Якщо ви пишете таким чином $K$ $K$

$\displaystyle \quad\ \bf{K_k} = \bf{P_k^-\, H_k^{\rm T} (H_k P_k^-\, H_k^{\rm T} + R_k)^{-1}} = \bf{\frac {P_k^-\, H_k^{\rm T}}{H_k P_k^-\, H_k^{\rm T} + R_k}}$

ви зрозумієте, що відносні величини матриць ( ) і ( ) контролюють співвідношення між використанням фільтра передбачуваною оцінкою стану ( ) та вимірюванням ( ). $R_k$ $P_k$ $x_{k}⁻$ $ỹ_k$

$\displaystyle \quad\ \lim\limits_{\bf{R_k \to 0}} \bf{{P_k^-\, H_k^{\rm T}} \over\ {H_k P_k^-\, H_k^{\rm T} + R_k}}\ = \bf{H_k^{-1}}$

$\displaystyle \quad\ \lim\limits_{\bf{P_k \to 0}} \bf{{P_k^-\, H_k^{\rm T}} \over\ {H_k P_k^-\, H_k^{\rm T} + R_k}}\ = \bf 0$

Заміна першої межі в рівняння оновлення вимірювання

$\displaystyle \quad\ \bf{\hat x_k} = \bf{x_k^-} + \bf{K_k}(\bf{\tilde y_k}-\bf{H_k}\bf{x_k^-})$

говорить про те, що коли величина невелика, що означає, що вимірювання точні, оцінка стану залежить в основному від вимірювань. $R$

Коли стан точно відомий, то невеликий порівняно з , і фільтр здебільшого ігнорує вимірювання, спираючись замість прогнозу, отриманого з попереднього стану ( ). $H P^⁻ H^T$ $R$ $x_k⁻$

— Jav_Rock
джерело

2

Спасибі! Якщо я маю рацію, не є щодо .

K_{k}

$K_k$

H_{k}

$H_k$

— Тім

12

Підвищення Калмана говорить вам про те, наскільки я хочу змінити свою оцінку за допомогою вимірювання.

${\bf S}_k$ - матриця розрахункової коваріації вимірювань . Це говорить нам про "мінливість" у наших вимірах. Якщо вона велика, це означає, що вимірювання сильно «змінюються». Тож ваша впевненість у цих вимірах низька. З іншого боку, якщо невелика , мінливість низька, наша впевненість у вимірюванні зростає. Коли ми впевнені у своїх вимірах, були впевнені, що інформація, яку ми отримуємо, є достатньою для нас, щоб оновити / змінити наші оцінки стану. Так виграш Кальмана вище. ${\bf z}_k$ ${\bf S}_k$

${\bf P}_k$ - матриця коваріаційного оцінювання стану. Це говорить нам про "мінливість" стану, . Якщо велика , це означає, що стан, за оцінками, сильно зміниться. Тому вам потрібно мати можливість змінювати свої оцінки за допомогою нових вимірювань. В результаті приріст Кальмана вищий. ${\bf x}_k$ ${\bf P}_k$

І навпаки, якщо невеликий, то ви знаєте, що ваш стан не змінюється настільки сильно, тому ви не хочете надто сильно змінювати свої оцінки в кожен момент. @ Відповідь Jav_Rock говорить, що якщо , то . Іншими словами, він мав на увазі, що якщо ви думаєте, що ваш стан більше не змінюється, ви більше не намагаєтесь змінювати свою оцінку. ${\bf P}_k$ ${\bf P}_k \rightarrow 0$ $K\rightarrow 0$

— ssk08
джерело

2

Jav_Rock отримав бал. Насправді, якщо ви пишете так $\bf{K_k}$

$\displaystyle \quad\ \bf{K_k} = \bf{P_k^-\, H_k^{\rm T} (H_k P_k^-\, H_k^{\rm T} + R_k)^{-1}} = \bf{H_k^-\frac {H_kP_k^-\, H_k^{\rm T}}{H_k P_k^-\, H_k^{\rm T} + R_k}}$

чисельник дробу означає невизначеність, поширювану з моделі, тоді як означає невизначеність вимірювання. Отже, значення дробу означає те, скільки нам слід довіряти вимірюванню, як пояснив Jav_Rock. $\bf{R_k}$

Що стосується , то воно просто перетворює спостереження назад у стан, тому що саме стан ми хочемо оновити, а не спостереження. $\bf{H_k^-}$

Щоб завершити, коефіцієнт посилення обчислює, скільки виправлень нам слід взяти від спостереження і перетворити корекцію спостереження назад у корекцію стану, що призводить до оновлення оцінки стану: $\bf{K_k}$

$\displaystyle \quad\ \bf{\hat x_k} = \bf{x_k^-} + \bf{K_k}(\bf{\tilde y_k}-\bf{H_k}\bf{x_k^-})$

— Чічао Чжан
джерело

-1

Я працюю над алгоритмом фільтра Кальмана (KF). Я помітив, що коефіцієнт посилення кальмана має справу з конвергенцією алгоритму з часом, тобто наскільки швидко алгоритм виправляє та мінімізує залишковий.

Приходячи до рівняння, виберіть початкове значення коефіцієнта посилення кальмана та змініть його від низького до високого, що може дати вам приблизне значення.

— Харша
джерело