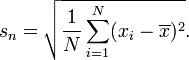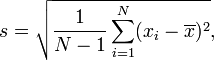Чому в школах США та Великобританії викладають різні методи обчислення стандартного відхилення?

15

Як я розумію, школи у Великобританії вчать, що стандартне відхилення можна знайти за допомогою:

$alt текст$

В той час як американські школи вчать:

$alt текст$

(на базовому рівні все одно).

Це спричинило ряд проблем моїх студентів у минулому, коли вони шукали в Інтернеті, але знайшли неправильне пояснення.

Чому різниця?

За допомогою простих наборів даних говорять про 10 значень, яка ступінь помилки буде, якщо застосовано неправильний метод (наприклад, на іспиті)?

— Амос
джерело

4

Я не впевнений, чи характеризувати ту чи іншу формулу як «неправильну» - це спосіб зрозуміти проблему. Просто другий є «кращим» у тому сенсі, що він є неупередженим оцінником справжнього стандартного відхилення. Отже, якщо ви дбаєте про неупереджені оцінки, то другий - "кращий" / "правильний".

Я характеризував формулу як "неправильну" суто в тому сенсі, що в іспиті, якщо ви використовуєте формулу, не заборонену програмою, ви отримаєте "неправильну" відповідь. Плюс, якщо значення самі по собі не є вибіркою сукупності, то, безумовно, перша формула дає більш точне значення.

— Амос

14

Срікант, я не думаю, що другий - це об'єктивний оцінювач. Квадрат його - неупереджений оцінювач справжньої дисперсії. Однак нерівність Дженсена встановлює, що очікування криволінійної функції випадкової величини не те саме, що функція очікування випадкової величини. Отже, друга формула не може бути неупередженою оцінкою справжнього стандартного відхилення.

— Ендрю Робінсон

Для перехресного посилання: його також запитали @ m.SE ...

— JM не є статистиком

4

Будь-яка школа США , використовуючи дуже популярний елементарний текст Фрідмана, Пізані, і Первс використовує першу формулу (

), так що здається неправильним характеризувати це як різницю в США проти Великобританії.

s_{n}

$s_n$

— whuber

18

Перша формула - це стандартне відхилення сукупності, а друга формула - стандартне відхилення вибірки . Друга формула також пов'язана з неупередженим оцінювачем дисперсії - детальнішу інформацію див. У Вікіпедії .

Я думаю (тут) у Великобританії вони не розрізняють вибірки та чисельність у середній школі. Вони, звичайно, не торкаються таких понять, як упереджені оцінки.

— csgillespie
джерело

4

Колін, неупереджений оцінювач стандартного відхилення не має в загальному випадку представлення закритої форми. Існує неупереджений оцінювач варіації (s 2 в даному випадку). Зазначимо, що обидва є послідовними оцінками дисперсії сукупності - і так за теоремою безперервного відображення є двома оцінками стандартних відхилень. Пов'язаний момент полягає в тому, що s n 2 має менший MSE, ніж s 2 . Додаткова перевага від нав'язування неупередженості є спірною.

— Стріттон

@Tirthankar - дуже неохайний мене. Відповідь я трохи змінив. Спасибі.

— csgillespie

2

Наскільки я пам’ятаю, мене навчали «вибірковому» обчисленню в математиці та науці GCSE (вік 14-16 років), і відмінність між популяціями та зразками та пов'язаними з ними мірками дисперсії було охоплено (хоча і не глибоко) на рівні А ( вік 16-18). Тому я не впевнений, що це проста різниця у Великобританії та США.

— Фрея Гаррісон

11

Тому що ще ніхто не відповів на остаточне запитання, а саме - кількісно відмінності між двома формулами - давайте подбаємо про це.

З багатьох причин доцільно порівнювати стандартні відхилення з точки зору їх співвідношень, а не їх відмінностей. Співвідношення є

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

Наближення можна розглядати як обрізання (чергується) ряду Тейлора для квадратного кореня, що вказує на помилку не може перевищувати $|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ $2$

$N$ $5$ $N$ $10$ оцінок або прогнозів (наприклад, використання 68-95 -99,7 правило). Розбіжності є ще менш важливими при порівнянніSD, наприклад, при порівнянні спредів двох наборів даних. (Коли набори даних є нескінченними, розбіжності фактично зникають зовсім, і обидві формули призводять до однакових висновків.) Можливо, це такі міркування, яких ми намагаємось навчити початківців, тому, якщо студенти переймаються питанням, яку формулу використовувати, це може бути сприйнято як знак того, що текст чи клас не підкреслюють те, що є дійсно важливим.

$N$ $t$ $z$ $s$ $s_n$

— дзижчати
джерело

6

Це виправлення Бесселя . У американській версії показана формула стандартного відхилення вибірки , де версія Великобританії вище - це стандартне відхилення вибірки .

— Рід Копсі
джерело

5

Я не впевнений, що це суто американське та британське питання. Решта цієї сторінки витягнута з написаного нами файлу ( http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 ).

Як обчислити СД з n-1 у знаменнику

Обчисліть квадрат різниці між кожним значенням і середнім значенням вибірки.
Додайте ці значення.
Розділіть суму на n-1. Результат називається дисперсією.
Візьміть квадратний корінь, щоб отримати Стандартне відхилення.

Чому n-1?

Навіщо ділити на n-1, а не на n при обчисленні стандартного відхилення? На кроці 1 ви обчислюєте різницю між кожним значенням і середнім значенням цих значень. Ви не знаєте справжнього значення серед населення; все, що ви знаєте, - це середнє значення для вашого зразка. За винятком рідкісних випадків, коли середня вибіркова сума дорівнює середній сукупності, дані будуть ближче до середнього рівня вибірки, ніж будуть до справжнього середнього значення сукупності. Таким чином, значення, яке ви обчислюєте на кроці 2, ймовірно, буде трохи меншим (і не може бути більшим), ніж те, яке було б, якби ви використовували справжнє значення сукупності на кроці 1. Щоб компенсувати це, розділіть на n-1 ніж nv Це називається корекцією Бесселя.

Але чому n-1? Якби ви знали середнє значення вибірки та всі значення, окрім одного, ви могли б обчислити, яким має бути останнє значення. Статистики кажуть, що існує n-1 ступінь свободи.

Коли SD слід обчислювати знаменник n замість n-1?

У статистичних книгах часто в знаменнику відображаються два рівняння для обчислення SD, одне за допомогою n, а друге за допомогою n-1. Деякі калькулятори мають дві кнопки.

Рівняння n-1 використовується в загальній ситуації, коли ви аналізуєте вибірку даних і хочете зробити більш загальні висновки. Таким чином, обчислений SD (з n-1 в знаменнику) - найкраща здогадка про значення SD у загальній сукупності.

Якщо ви просто хочете кількісно визначити варіацію певного набору даних, і не плануєте екстраполювати, щоб робити більш широкі висновки, тоді ви можете обчислити SD, використовуючи n у знаменнику. Отриманий SD - це SD цих конкретних значень. Немає сенсу обчислювати СД таким чином, якщо ви хочете оцінити рівень населення, з якого виходили ці точки. Має сенс використовувати n в знаменнику лише тоді, коли немає вибірки з популяції, немає бажання робити загальні висновки.

Мета науки майже завжди полягає в узагальненні, тому рівняння з n в знаменнику не слід використовувати. Єдиний приклад, який я можу придумати, де це може мати сенс, - це кількісна оцінка варіації серед балів екзамену. Але набагато краще було б показати розсіювач кожного бала або гістограму розподілу частоти.

— Харві Мотульський
джерело

1

Я не припускав, що це було, мені було просто цікаво, чому така різниця могла виникнути, який рівень помилки внаслідок помилкових порад може дати і чи є гідне пояснення різниці, яку я можу дати своїм студентам .

— Амос

@harvey - посилання мертве

— baxx

1

@baxx .. Дякуємо, що вказали на це. Виправлено.

— Харві Мотульський

3

Оскільки N - кількість точок у наборі даних, можна стверджувати, що шляхом обчислення середнього зменшився ступінь свободи в наборі даних на одиницю (оскільки один ввів залежність у набір даних), тож слід використовувати N -1 при оцінці стандартного відхилення від набору даних, за яким доводилося оцінювати середнє значення раніше.

— Бенджамін Баньє
джерело