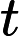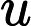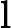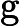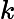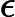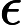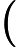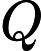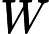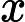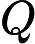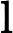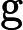Чому так мало природних кандидатів на статус проміжного NP?

29

Теорема Ладнера добре відома, що якщо , то існує нескінченно багато проміжних ( ) задач. Також є природні кандидати на цей статус, такі як Графічний ізоморфізм та ряд інших, див. Проблеми між P та NPC . Проте, переважна більшість в натовпі відомої -проблеми , як відомо, бути або в або . Лише невелика частка з них залишається кандидатом у ${\mathsf P}\neq \mathsf {NP}$ $\mathsf {NP}$ $\mathsf{NPI}$ $natural$ $\mathsf {NP}$ $\mathsf {P}$ $\mathsf {NPC}$ $\mathsf {NPI}$ . Іншими словами, якщо ми випадково вибираємо природну проблему серед відомих, у нас є дуже мало шансів вибрати кандидата Чи є якесь пояснення цьому явищу? $\mathsf {NP}$ $\mathsf {NPI}$

Я міг би придумати 3 можливі пояснення, докладніше з філософської сторони:

Причиною виникнення такої невеликої частки природних кандидатів у є те, що часом виявиться порожнім. Я знаю, це означає , тому це дуже малоймовірно. Тим не менш, можна все-таки стверджувати (хоча я не один з них), що рідкісність природних проблем - це емпіричне спостереження, яке, схоже, насправді підтримує , на відміну від більшості інших спостережень. $\mathsf {NPI}$ $\mathsf {NPI}$ ${\mathsf P} =\mathsf {NP}$ $\mathsf {NPI}$ ${\mathsf P} =\mathsf {NP}$
Трохи «природно - » є вид різкого фазового переходу між легкої і важкою проблемою. Мабуть, осмислені, природні алгоритмічні проблеми поводяться так, що вони, як правило, легкі або важкі, перехід вузький (але все ще існує). $\mathsf {NPI}$
Аргумент у 2 можна довести до крайності: врешті-решт всі проблеми в "природному " будуть поставлені в , поки , так . Це означало б, що всі проблеми, що залишилися в $\mathsf {NPI}$ $\mathsf {P} \cup \mathsf {NPC}$ ${\mathsf P}\neq \mathsf {NP}$ $\mathsf {NPI}\neq \emptyset$ $\mathsf {NPI}$ є "неприродними" (надуманими, без сенсу реального життя). Тлумачення цього може бути таким, що природні проблеми є легкими або важкими; перехід - лише логічна конструкція, без «фізичного» значення. Це дещо нагадує випадок ірраціональних чисел, які цілком логічні, але не виникають як вимірюване значення будь-якої фізичної величини. Як такі вони не походять від фізичної реальності, скоріше знаходяться в "логічному закритті" цієї реальності.

Яке пояснення вам найбільше подобається чи ви можете запропонувати інше?

cc.complexity-theory p-vs-np np-intermediate

— Андрас Фараго
джерело

13

Гм, довжина діагоналі квадрата 1см х 1см - це ірраціональне число ...

— Джошуа Грохов

4

Також вам може бути цікаво, що в теорії обмежених ресурсами мір збір NP-повних множин має p-міру 0. Іншими словами, p-випадкові множини в NP не є NP-повними. Дійсно, це стосується будь-якого багаточлена багато-одного ступеня. (Міра збору всіх наборів НП є відкритим питанням: якщо вона не є нульовою, або не вимірюється, тоді

)

P \neq N P

$\mathsf{P} \neq \mathsf{NP}$

— Джошуа Грохов

7

відповідь пов'язана з тим, які проблеми ми вважаємо "природними", що є досить філософським питанням. також не зовсім зрозуміло, що передумова цього питання дотримується: багато проблем, що виникають внаслідок криптографії, мають проміжну складність. нарешті, те, що ви говорите про ірраціональні числа, є абсурдним.

— Сашо Ніколов

26

Як зазначали інші, дискусійним є те, наскільки річ, яку ви намагаєтесь пояснити, навіть правдива. Можна стверджувати, що в 60-70-х роках теоретиків-комп’ютерів просто більше цікавили різновиди проблем, які виявляються як у П, так і в НП. Сьогодні, через наростання теоретично-теоретичної криптографії, квантових обчислень, решіток тощо. - а також простого факту, що NP-повнота настільки добре зрозуміла --- ми все більше і більше цікавитесь види проблем, які виявляються NP-проміжними.

Все-таки можна запитати: наскільки річ є правдою --- тобто настільки, що стільки проблем із природним пошуком та оптимізацією «оснащуються» до того, що вони є NP-завершеними, або ж таки P в цій мірі , чому це правда? Тут я думаю, що ви можете отримати багато інтуїції, дивлячись на більш раннє явище з обчислюваності: що стільки природних моделей обчислень "оснащуються" до того, щоб Тюрінг був повним. У цьому випадку, я б сказав , що пояснення полягає в тому, що, як тільки у вас є кілька основних компонентів --- пам'ять читання / запису, петлі, умовними і т.д. .--- це важко уникатиможливість імітувати машину Тьюрінга, а отже, бути Тюрінгом. Так само, як тільки ваша проблема пошуку чи оптимізації містить декілька основних компонентів --- головне, можливість конструювати "гаджети", що імітують логічні ворота типу AND, OR, AND NOT --- важко уникнути можливості для кодування SAT і, таким чином, є NP-повним.

Як мені подобається думати про це, такі проблеми, як SAT, чинять потужне «гравітаційне тягнення» до всіх інших обчислювальних проблем, що знаходяться в їх околицях, змушуючи їх захотіти «піднятися» і до NP-завершення. Отже, зазвичай навіть не потрібно спеціальних пояснень, коли ще одна проблема піддається цьому потягу! Що більш вражаюче і більше потребує пояснень - це коли (мабуть) важка проблема NP має деяку властивість, яка дозволяє йому протистояти гравітаційному тягу SAT. Тоді ми хочемо знати: що це за властивість? Чому ви не можете зіграти звичайний трюк NP-повноти для цієї проблеми, створити гаджети, що кодують булеві логічні ворота? У цій останній відповіді CS.SE я склав список деяких поширених відповідей на це питання, але (як уже вказав інший коментатор) є й інші можливі відповіді, які я пропустив.

— Скотт Ааронсон
джерело

Також актуальною для останньої частини є питання Скотта cstheory.stackexchange.com/questions/19256/…

— András Salamon

17

Багато природних проблем можна виразити як проблеми задоволення обмеженнями, а для ДСП є теореми про дихотомію.

— Джошуа Грохов
джерело

9

Просто жарт: подумавши про "гравітаційне тягнення SAT" у приємній відповіді Скотта Аронсона, на думку мені прийшла ще одна метафора: 3-SAT 2-SAT сендвіч !

введіть тут опис зображення

$(2 + \frac{(\log n)^k}{n^2})$

$(2+1/n^{2−\epsilon}),0<\epsilon<2$

$(2+f(n))$

— Марціо Де Біасі
джерело

3

(2 + ε)

$(2+\varepsilon)$

(2 + f (n))

$(2+f(n))$

(2 + 1 / n^{2 - ϵ}), 0 < ϵ < 2

$(2+1/n^{2-\epsilon}), 0<\epsilon<2$

(2 + ϵ)

$(2+\epsilon)$

3

(2 + f (n))

$(2+f(n))$

1

@MarzioDeBiasi вам слід розглянути можливість додавання цих двох посилань безпосередньо до вашої відповіді (де їх можна шукати), а не ховати їх у коментарях.

— Артем Казнатчеєв

8

$NP$ $NP$ $NP$ $NP$ $P \ne NP$

$NP$ $NP$ $NP$

$NP$ $FPT \ne W[1]$

Список літератури :

1- М. Грохе. Складність проблем гомоморфізму та обмеженості задоволення, що спостерігаються з іншого боку. Журнал ОСББ, 54 (1), стаття 1, 2007

2- Пітер Джонсон, Віктор Лагерквіст і Густав Норд. Видування отворів у різних аспектах обчислювальних задач із додатками для обмеження задоволення. У матеріалах 19-ї міжнародної конференції з принципів та практики програмування обмежень (CP-2013). 2013 рік.

— Мухаммед Аль-Туркстані
джерело

1

чому ці проблеми з ДСП не підпадають під гіпотезу дихотомії?

— Сашо Ніколов

1

Чи обмеження ширини ширини, як в результаті Grohe, насправді природне? (Питання не риторичне - я, чесно кажучи, не знаю.) На мою думку, споруди Джонсон-Лагерквсіт-Норд здаються лише дещо природнішими, ніж у Ладнера. Я думаю, що пункт у вашому першому абзаці є відмінним.

— Джошуа Грохов

@JoshuaGrochow Я боюся, що це сперечається, оскільки не існує офіційного поняття про те, які природні засоби.

— Мохаммед Аль-Туркстані

@SashoNikolov Ви маєте на увазі припущення про дихотомію Федера та Варді?

— Мохаммед Аль-Туркстані

1

A

$A$

_

$\_$

_

$\_$

B

$B$

7

Ось казка про структуру НП-проміжних проблем Златилоцького. (Попередження: ця історія може бути корисною помилкою для генерування та перевірки потенційних гіпотез, але не має бути науково суворою. Вона спирається на одну частину Експоненціальна гіпотеза часу, дефіс магії складності Колмогорова, деякі фрагменти, запозичені з теорії САТ вирішення та евристична трихотомія Теренса Тао щодо проблем. Споживайте на власний ризик, як і всі махові маски щодо математики.)

Якщо майже всі екземпляри проблеми в NP мають структуровану структуру, то проблема є насправді в P. Таким чином, майже всі випадки містять багато надмірності, а алгоритм поліноміального часу для проблеми - це спосіб визначити надмірність. Можна навіть уявити, що кожну проблему в P можна отримати, взявши якусь проблему в EXP і додавши структуровану надмірність, через якусь форму прокладки (не обов'язково звичайного виду). Якби це було так, то алгоритм поліноміального часу може розглядатися як ефективний спосіб скасувати це прокладка.

Якщо є достатньо екземплярів, які не структуровані, утворюючи "серцевину твердості", то проблема є NP-завершеною.

Однак, якщо ця "серцевина твердості" є надто рідкою, то вона має лише можливість представити частину SAT, тому проблема полягає в P або NP-проміжних. (Цей аргумент - суть теореми Ладнера). Щоб використати аналогію Скотта, "серцевина твердості" справляє гравітаційну тягу до проблеми, до того, що вона є повною NP. Екземпляри в "ядрі твердості" не містять великої надмірності, і єдиний реалістичний алгоритм, який працює для всіх цих примірників, - це пошук грубої сили (звичайно, якщо їх є лише кінцево багато, то і пошук таблиць також працює).

З цієї точки зору, проблеми, пов'язані з проміжними показниками NP, повинні бути рідкісними на практиці, оскільки для них потрібен тонкий баланс Золотокрилих між структурованими та неструктурованими екземплярами. Примірники повинні мати достатню надмірність, щоб вони частково піддавалися алгоритму, але має бути достатньо ядра твердості, щоб проблема не була в П.

Можна розповісти ще простішу (і кумедну, але також потенційно ще більш оманливу) історію на основі головоломок. Маючи лише кілька обмежень, можна змусити здійснити багато пошуку, наприклад, NxN Sudoku не завершений NP. Тепер розглянемо, як вам запропонують вирішити безліч маленьких головоломок як один екземпляр за один раз (наприклад, багато 9x9 Sudokus). Затрачений час буде приблизно лінійним за кількістю головоломок у кожному екземплярі, і ця проблема тоді в П. Для проміжних проблем можна думати, що кожен екземпляр є великим (але не надто великим) числом Sudokus на великій мові (але не надто великі) сітки. Причина, по якій ми не спостерігаємо багатьох подібних проблем, полягає в тому, що вони були б скупі поставити і вирішити!

— Андраш Саламон
джерело

1

L

$L$

C

$C$

L

$L$

k

$k$

n^{k} + k

$n^k + k$

C

$C$

L \notin P

$L \notin \mathsf{P}$

L

$L$ ) гіпотеза, що мови в НП з досить щільними ядрами повинні бути повноцінними NP.

— Джошуа Грохов

1

У згадках, які Джошуа згадував: Lynch: dx.doi.org/10.1145/321892.321895 та Orponen-Schöning: dx.doi.org/10.1016/S0019-9958(86)80024-9 також див. Orponen-Ko-Schöning-Watanabe: dx. doi.org/10.1145/174644.174648

— András Salamon

2

$\mathsf{NPI}$ $\mathsf{NPI}$ $\mathsf{NP}$

$n$ $\geq \log n$ $\mathsf{NPI}$ $\mathsf{NP}$ $x$ $Q$ $x$ $Q$ $\mathsf{NPI}$ $\mathsf{P}$

$\mathsf{NPI}$ $\mathsf{NP}$ $\mathsf{NPI}$ $\mathsf{NPC}$

$\mathsf{NPI}$ $\mathsf{P}$

— Андрас Фараго
джерело

3

W [1]

$W[1]$

x

$x$

Q

$Q$

x

$x$

O (\log | x |)

$O(\log |x|)$

Що стосується 3-КОЛОРОВОГО, що таке зменшена версія проблеми?

— Андрас Саламон

1

n

$n$

\log n

$\log n$

2

Це не різниця в / б "бути клікою" і "бути 3-кольоровою". Різниця між початковою проблемою полягає в тому, що: 1) чи має граф підграф з деяким властивістю заданого розміру (наприклад, CLIQUE) проти 2) чи має графік властивість. У випадку (1) зміни розміру для журналу є природним, b / c розмір підграфа вже був частиною питання. Коли ви зробите свою хитрість до (2), ви додасте розмір підграфу як нову частину проблеми.

— Джошуа Грохов