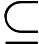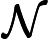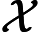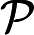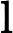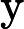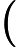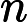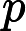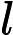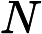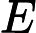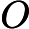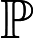Нерозумна сила нерівномірності

З точки зору здорового глузду, легко повірити, що додавання недетермінізму до значно розширює його силу, тобто набагато більше, ніж . Адже недетермінізм дозволяє експоненціальний паралелізм, який, безперечно, видається дуже потужним. Н П $\mathsf{P}$$\mathsf{NP}$$\mathsf{P}$

З іншого боку, якщо ми просто додамо нерівномірність до , отримуючи , то інтуїція є менш зрозумілою (якщо припустити, що ми виключаємо нерекурсивні мови, які могли виникнути в ). Можна було очікувати, що просто дозволити різні алгоритми поліноміального часу для різної вхідної довжини (але не залишати рекурсивну область) є менш потужним розширенням, ніж експоненціальний паралелізм у недетермінізмі.П / п о л $\mathsf{P}$$\mathsf{P}/poly$$\mathsf{P}/poly$

Цікаво, однак, якщо ми порівнюємо ці класи з дуже великим класом , то ми бачимо наступну протиінтуїтивну ситуацію. Ми знаємо, що правильно містить , що не дивно. (Зрештою, дозволяє вдвічі експоненціальний паралелізм.) З іншого боку, наразі ми не можемо виключити .$\mathsf{NEXP}$$\mathsf{NEXP}$ $\mathsf{NP}$$\mathsf{NEXP}$$\mathsf{NEXP}\subseteq \mathsf{P}/poly$

Таким чином, у цьому сенсі нерівномірність, додана до часу полінома, можливо робить його надзвичайно потужним, потенційно більш потужним, ніж недетермінізм. Це навіть може зайняти симуляцію подвійного експоненціального паралелізму! Незважаючи на те, що ми вважаємо, що це не так, але той факт, що в даний час це неможливо виключити, все ще говорить про те, що теоретики складності борються з "могутніми силами" тут.

Як би ви пояснили розумному мирянину, що стоїть за цією «необґрунтованою силою» нерівномірності?

Відповідь фліп полягає в тому, що це не перше, що стосується теорії складності, що я б спробував пояснити лайперсону! Щоб навіть оцінити ідею нерівномірності та наскільки вона відрізняється від недетермінізму, вам потрібно бути далі в бур’янах з визначеннями класів складності, ніж багато людей готові отримати.

Сказавши це, одна точка зору, яку я вважаю корисною, пояснюючи студентам P / poly, полягає в тому, що нерівномірність насправді означає, що ви можете мати нескінченну послідовність кращих і кращих алгоритмів, оскільки ви переходите до більшої та більшої довжини введення. На практиці, наприклад, ми знаємо, що алгоритм множення матричних матриць найкраще працює для матриць розміром 100x100 або більше, а потім в якийсь момент множення Страссена стає кращим, і тоді новітні алгоритми стають кращими лише для астрономічно великих матриць, які ніколи не виникне на практиці. Отже, що робити, якщо у вас була магічна здатність до нуля за найкращим алгоритмом для будь-якого діапазону росіян, з яким ви мали справу?

Звичайно, це була б дивна здатність, і все, що розглядається, мабуть, не настільки корисне, як здатність вирішувати задачі, повні з NP, у поліноміальний час. Але строго кажучи, це було б незрівнянною здатністю: це не те, що ви отримаєте автоматично, навіть якщо P = NP. Дійсно, ви навіть можете побудувати надумані приклади нерозбірливих проблем (наприклад, якщо вводити 0 ⁿ як вхід, чи зупиняється п- ^я машина Тюрінга?), Яку ця здатність дозволила б вам вирішити. Отже, це сила нерівномірності.

Щоб зрозуміти сенс розгляду цієї дивної сили, вам, мабуть, потрібно буде сказати щось про квест, щоб довести нижню межу схеми, і про те, що, з точки зору багатьох наших методів нижньої межі, однаковість здається дивною додаткова умова, яка нам майже ніколи не потрібна.

Ось аргумент "гладкості", який я нещодавно почув на захист твердження, що нерівномірні моделі обчислення повинні бути більш потужними, ніж ми підозрюємо. З одного боку, із теореми часової ієрархії ми знаємо, що існують, наприклад, функції, обчислювані у часі , які не обчислюються у часі . З іншого боку, за теоремою Лупанова будь-яка булева функція на входах обчислюється схемою розміру . Отже, якщо ми стверджуємо, що нерівномірність не дає великої сили, тобто повинен вести себе як , то це позов повинен різко припинити тримання, колиO ( 2 n ) n ( 1 + o ( 1 ) ) 2 n / n S I Z E ( f ( n ) ) D T I M E ( f ( n ) O ( 1 ) ) f ( n $O(2^{2n})$$O(2^{n})$$n$$(1+o(1))2^n/n$$\mathsf{SIZE}(f(n))$$\mathsf{DTIME}(f(n)^{O(1)})$$f(n)$стає . Але така поведінка - два заходи складності йдуть рука об руку, поки раптом один із них не стає всесильним --- здається довільним і дещо неприродним.$2^{O(n)}$

З іншого боку, якщо схеми є достатньо потужними, що , то за Карпа-Ліптона ієрархія поліномів руйнується до другого рівня, що також буде дивним: чому квантифікатори раптом перестати давати обчисленням більше сили? Я не впевнений, де це нас залишає.$\mathsf{NP} \subseteq \mathsf{P/poly}$

Я припускаю, що говорити з ким-небудь про та означає, що людина знайома з питанням vs та подвійністю перевірки та вирішенням.Н П Р Н $\mathbb{P/poly}$$\mathbb{NP}$$\mathbb{P}$$\mathbb{NP}$

Потім я спробую пояснити, що настільки потужний, оскільки для кожної різної довжини ТМ отримує поради, що йому можна повністю довіряти. Тоді я хотів би зазначити, що ми можемо розробити жорсткі (фактично не TM-обчислювані фактично) мови, які мають 1 слово на вхідну довжину (тобто одинарний), тому вони знаходяться в P / poly! Але, можливо, довготривалої ради з полином недостатньо для вирішення всіх мов у , оскільки там нам дозволено різний натяк на кожен різний вклад.Н $\mathbb{P/poly}$$\mathbb{NP}$

З іншого боку, я нагадаю цій людині, що має перевірити відповідь, а не довіряти їй повністю. Отже, ми не можемо використовувати однакові поради для кожної довжини введення, це може бути неможливо перевірити!$\mathbb{NP}$

Нарешті, я зазначу, що теоретики складності вважають, що в існують мови, які потребують більше, ніж багаточлен, багато натяків на деяку вхідну довжину, і тому не можуть бути в .Р / п о л $\mathbb{NP}$$\mathbb{P/poly}$

Критичним моментом для хорошого розуміння, який, на мою думку, також є загальним при першому викладанні предмета, є зрозуміло, що поради та «підказки» (тобто сертифікат) - це різні речі, і чим вони відрізняються.

Для мене найяскравішою ілюстрацією сили нерівномірності є те, що відповідна додаткова версія проблеми зупинки вже в P / 1. Тоді достатньо одного порад поради, щоб визначити цю мову за допомогою тривіальної TM, яка просто повертає біт поради.

Звичайно, викладення невідкладної мови експоненціальною сумою означає, що це не "морально" в P / poly. Але це свідчить про те, що потрібно бути обережними, дозволяючи нерівномірність.

У мене складається враження, що справжнє питання тут полягає в необґрунтованому важкому доказуванні, а не в необгрунтованій силі нерівномірності. Оскільки відповіді Хазісопа та Андраша Саламона вже наголошують, нерозбірливі мови стають обчислювальними навіть у дуже обмежених неоднорідних мовах, оскільки тягар доказування повністю відмовився.

Основна інтуїція, чому ми можемо піти без доказів, - це лише різних входів довжиною , на які ми повинні перевірити, чи схема дає правильну відповідь. Тож, схоже, було б доказ максимум експоненціальної довжини в , що схема дійсно дає правильну відповідь. Але це справедливо лише до тих пір, поки для кожного вводу довжини існує доказ щонайбільше експоненціальної довжини в , що вхід (не) міститься в мові (якщо він фактично (не) міститься в мові) . Зауважимо, що експоненціально багато входів разів максимум експоненціально довгий доказ для кожного входу дає повний доказ для всіх входів експоненціальної довжини, оскільки n n n n 2 n exp ( O ( n ) ) = exp ( n log ( 2 ) + O ( n ) ) = exp ( O ( n ) $2^n$$n$$n$$n$$n$$2^n\exp(O(n))=\exp(n\log(2)+O(n))=\exp(O(n))$ .

Якщо нам потрібно існувати доказ максимум експоненціальної довжини в для неоднорідних мов, то ми можемо довести, що всі ці мови містяться в . Відповідний недетермінований алгоритм просто потребує підказки, яка містить обидві «малі» схеми разом із «малим» доказом того, що ця схема дійсно обчислює те, що вона повинна обчислити.N E X $n$$\mathsf{NEXP}$

Той самий недетермінований алгоритм також показав би , якщо ми вимагатимемо замість цього існувати докази довжини не більше полинома в що схема підходить. Зауважте, що цей обмежений все ще може бути більш потужним, ніж . Навіть Карп-Ліптон (тобто, що ієрархія поліномів руйнується, якщо ) все-таки справедливий, але це твердження менш цікаве, ніж реальна теорема Карпа-Ліптона. n P / p o l y ′ P N P ⊆ P / p o l y $\mathsf{P/poly'}\subseteq \mathsf{NP}$$n$$\mathsf{P/poly'}$$\mathsf{P}$$\mathsf{NP}\subseteq\mathsf{P/poly'}$